数字で根拠を示せる営業マンって説得力や安心感があって、かっちょ良いですよね!そんな風になりたいものです。とはいっても、手元の色々なデータに対する分析しようにも、Σの計算なんてとっても面倒くさいですよね・・・。
大人のやりかたで仕事をしよう!
私達は高校生ではないので、大人のやりかたで簡単かつ短時間で仕事をこなしたいものです、大人のやり方とは、隣に本を置き、ネットで調べながら、ツールを駆使し最速で仕事をするということ。そこでお手持ちのエクセルを使うと、面倒な計算をすべてコンピュータの力で解決してくれるので、計算が苦手な人でも簡単に分析が出来ちゃうのです!
今回はポスティング件数と売上高から、相関関係を見出して、いくつポスティングすればどれだけ売上高が見込めるのかという簡単な未来を予測☆をしたいと思います。一般的な資料であれば、単回帰分析のデータで十分なはず。どこかのアンケート結果では、管理職の方のほとんどは単回帰分析で資料を作っているようですし、ビジネスで誰かに提案したり、見せる場合は複雑なデータより、わかりやすさが重要ですよね。
今回ご紹介する単回帰分析の要素はxとyの2つ、1次関数でとてもシンプル。しかし、売上高に繋がる条件が複数強く相関したり、3次だったり, 5次関数のグラフのほうが実態に適している場合もあります。話の頂点として、ビジネス的なわかりやすさと統計学的な正確性はトレードオフな場合があるということに注意が必要です。重回帰などの3つ以上の要素が絡むセクシーなデータを採用する場合は、専門知識がある人同士はOKですが、一般的なビジネスの提案用途としてはマニアックなデータになってしまい伝わらない危険性がありますよね。
作業フロー
- まずは月別の売上高の棒グラフを作成してみる
- xとyとして相関しそうな2つのデータを見つける
- 2つの相関比を計測する
→相関関係がない
おしまい、他のデータを見よう。 - 2つのデータから散布図を作成する
- 単回帰分析で1次関数を割り出す
- 1次関数を使って未来を予測する
こんな流れでやっていきます。
まずは、月別と売上高の棒グラフを作ろうね

単純に月別の売上高の棒グラフは資料作りの定番ですし、あったほうが現状を視覚的に俯瞰できて良いでしょう。
上記のようなデータがあったとします。
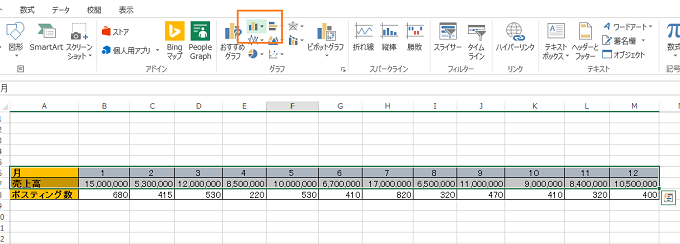
【挿入】>> 【グラフ】を選択します。
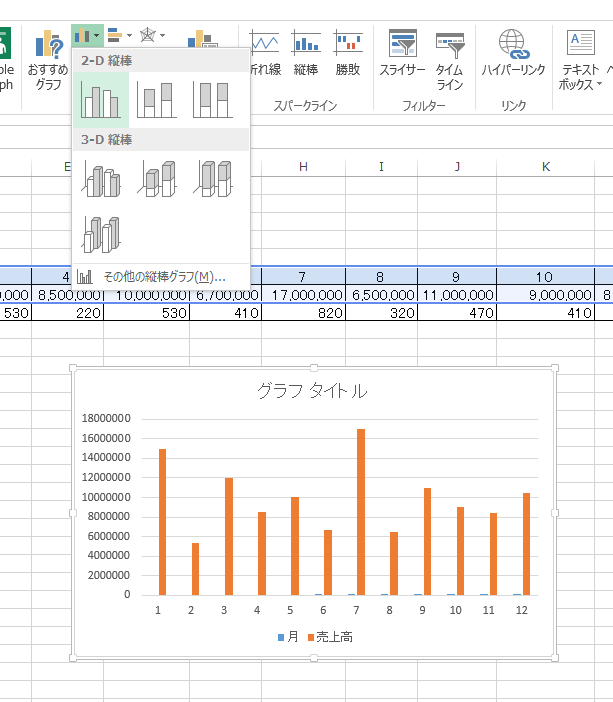
タイトルをつけましょうね。
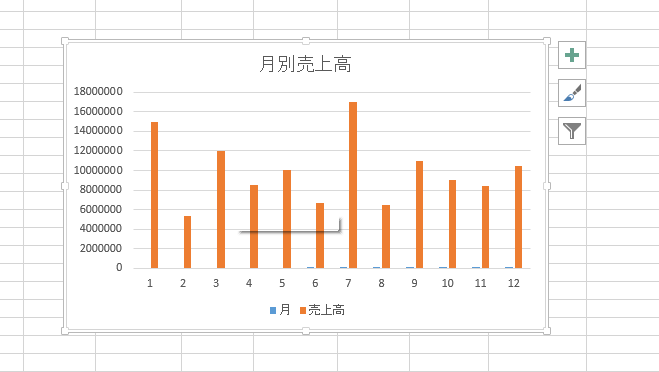
月別の売上高の推移が作れました。普通の一般的な月別の売上高でおなじみです。難しくないはずです。
ポスティング件数と売上高の関係性にせまる
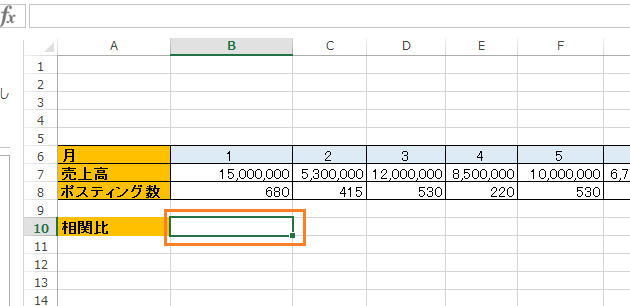
売上高とポスティング数の関係に相関関係がどれだけあるかという数値を計測します。
- ポスティング数が増えれば、売上高があがり
- ポスティング数が減れば、売上高は下がる
そういった関係があるのかというのが、CORREL関数を使うことで割り出せます。
相関比が出力されるセルを用意して、選択します。
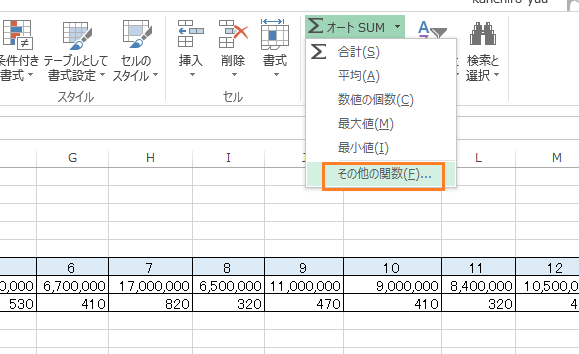
みんな大好き【オートSUM】の隣の▼タブをクリックして、【その他の関数】をクリックします。
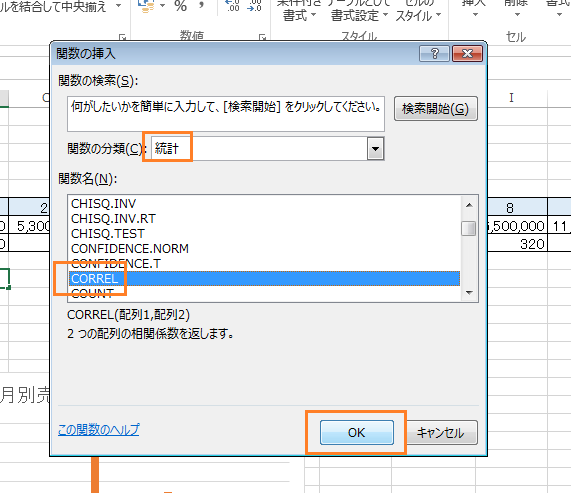
【関数の分類】のセレクトボックスから【統計】を選択し、『CORREL』関数を選択し、【OK】をクリックしましょう。
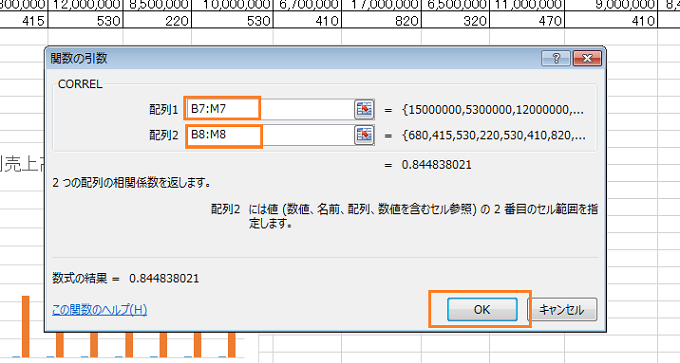
売上高の配列の範囲、ポスティング数の配列の範囲を指定して、【OK】をクリックします。
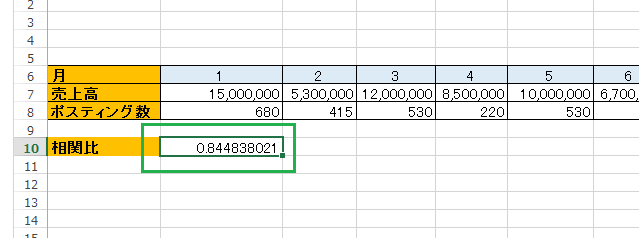
相関比が出ました。0.7以上あれば十分相関があると言えると思います。
相関の強さ
- 0.7~1 強い相関がある
- 0.4~0.69 やや相関がある
- 0.4以下 弱い相関がある
なんで相関比なんて出すの?
気温が高くなるとアイスクリームが売れる!のように、気温の上昇とアイスクリームの販売数など、2つのデータに対して、相関の関係性がないと分析する意味がないからです。相関比はその判断を数値化して行うことが出来ます。
散布図を作ろう!
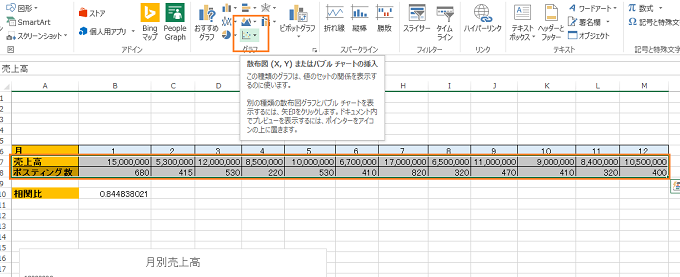
相関関係があるデータにおいて、散布図があるとデータの分布から、縦軸yと横軸xの規則性を確認・分析しやすいのです。
上記のように範囲して、【挿入タブ】>> グラフタブを選択します。
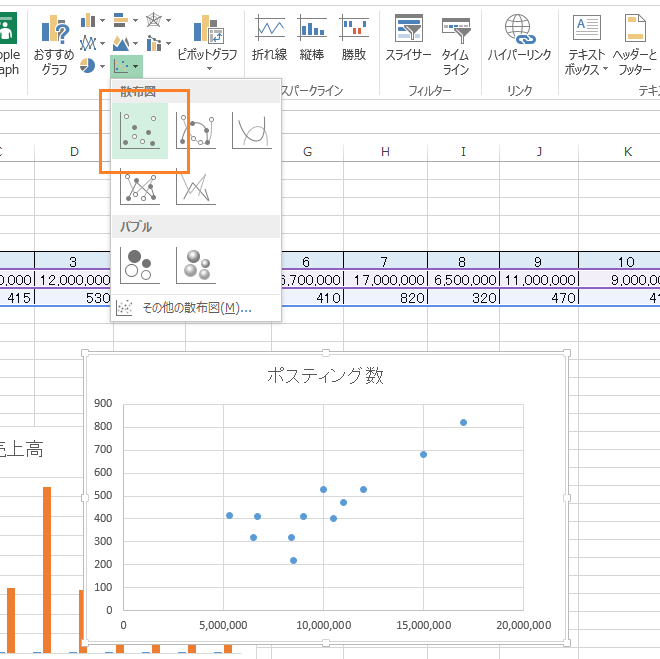
上記のように散布図を選択します。
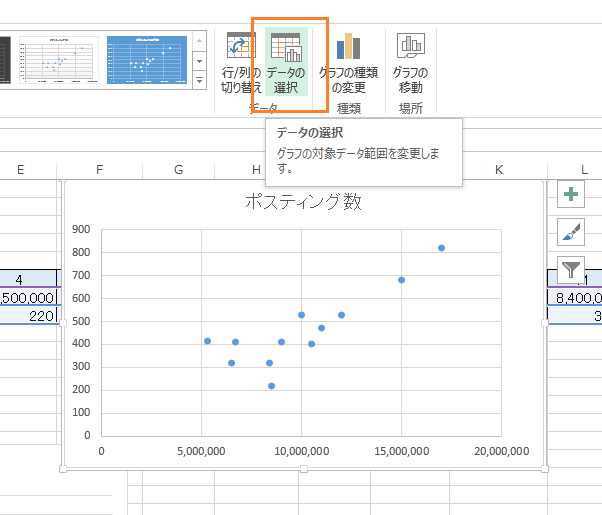
あらら、、x軸とy軸はx軸にポスティング数、y軸に売上高としたいのに、逆になっています。
そんな時は、【データの選択】をクリックして下さい。
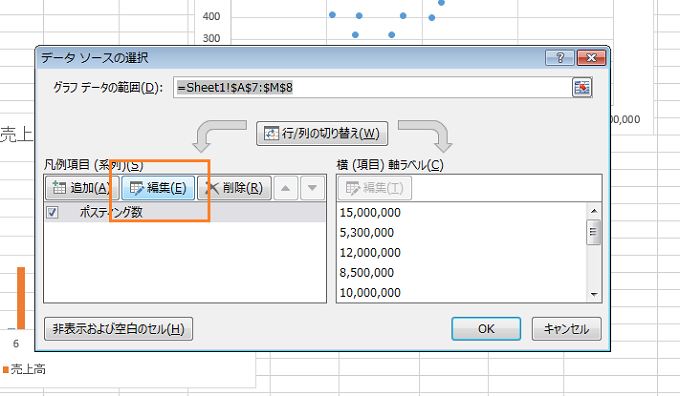
【編集】をクリックして下さいね!
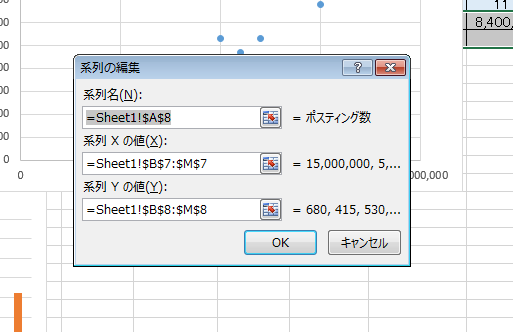
x軸とy軸の値はこうなっているので、
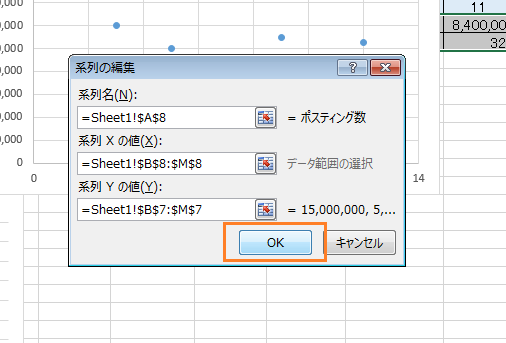
コピペで入れ替えてあげて下さい、入力が終わったら【OK】をクリックします。
【OK】をクリックします。
単回帰分析で未来を予測しよう!
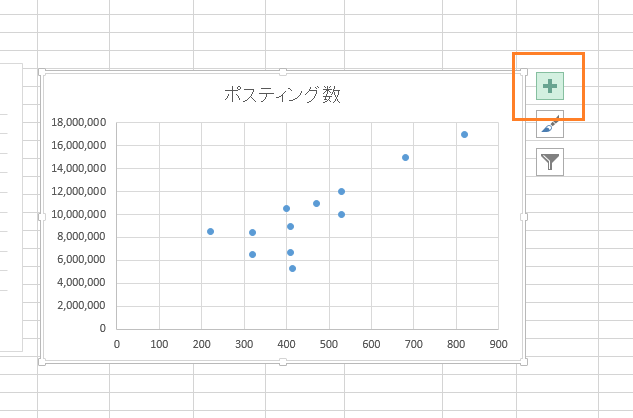
xとyの1次関数のグラフがこの段階で見えてきますね。
このグラフを具体的な数字を使って関数にしたいと思います、
相関するデータから関数にする=回帰分析
です。
近似的な関数をエクセルを使って割り出しましょ~!(もしアナログでおこないたいという場合は最小二乗法を使って、近似関数を割り出す必要があります。)
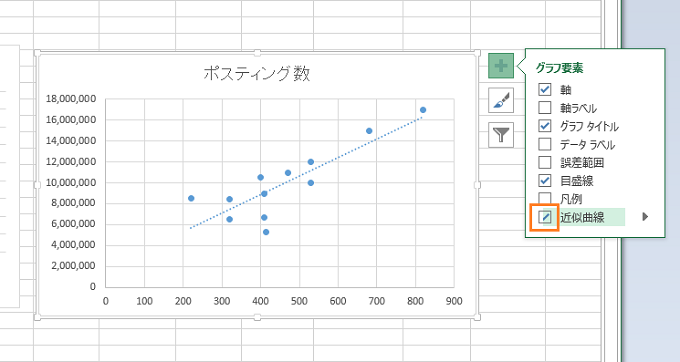
【近似曲線】をクリックします。
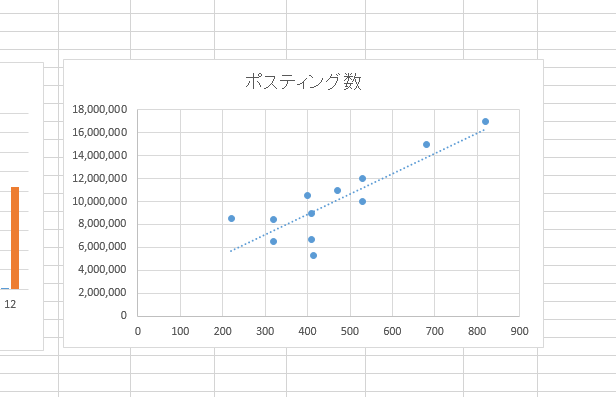
1次関数が出来ました。
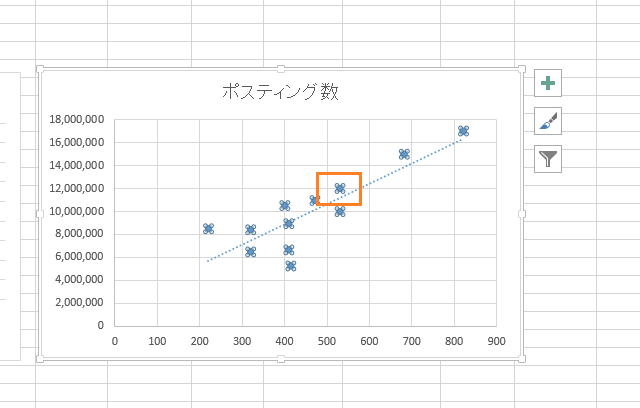
点をどれでも良いのでクリックして選択し、右クリックして下さい。
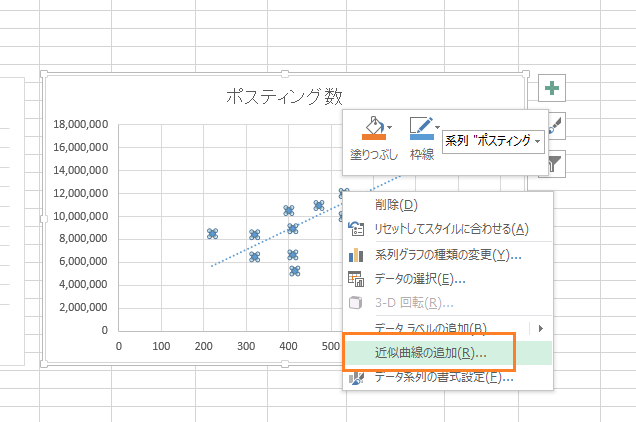
【近似曲線の追加】を選択します。
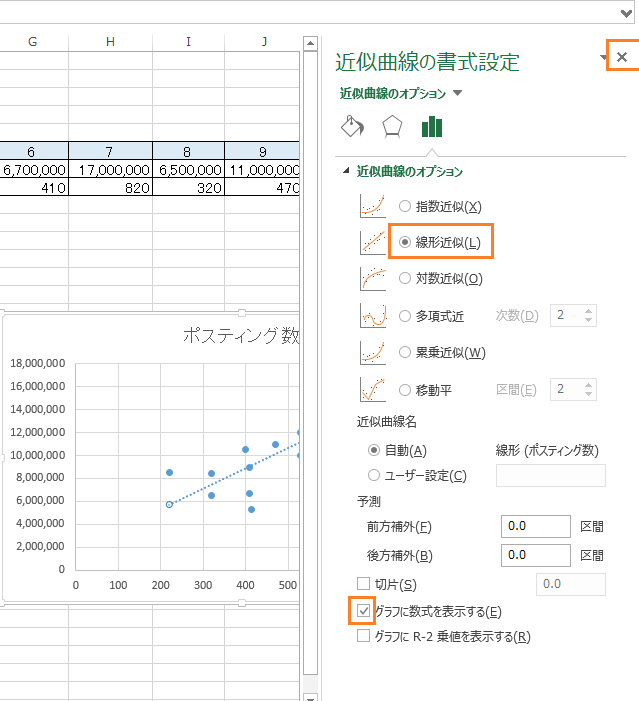
【線形近似】、【グラフに数式を表示する】をクリックして有効化して、【×】で閉じて下さいね!
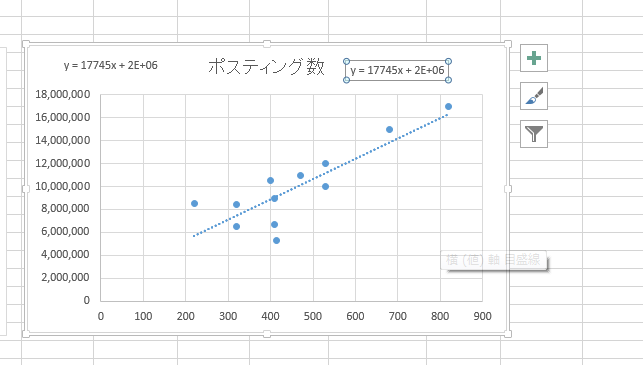
y=17745x + 2E+06
という関数が出来ました。
これはy = 17745x + 2×10の6乗を表します。
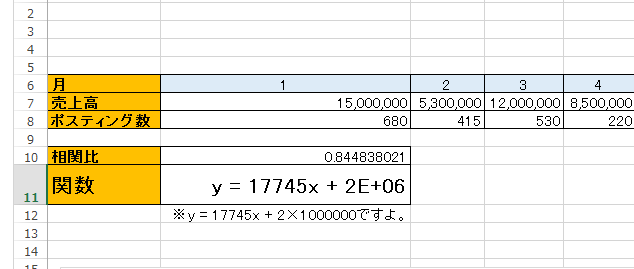
関数を使って未来を見通しちゃおう!

ポスティング数500の時に、10,872,500円の売り上げが見込めそうだなということがわかりますね!
どれだけ関数が実態に当てはまっているか確認しよう!
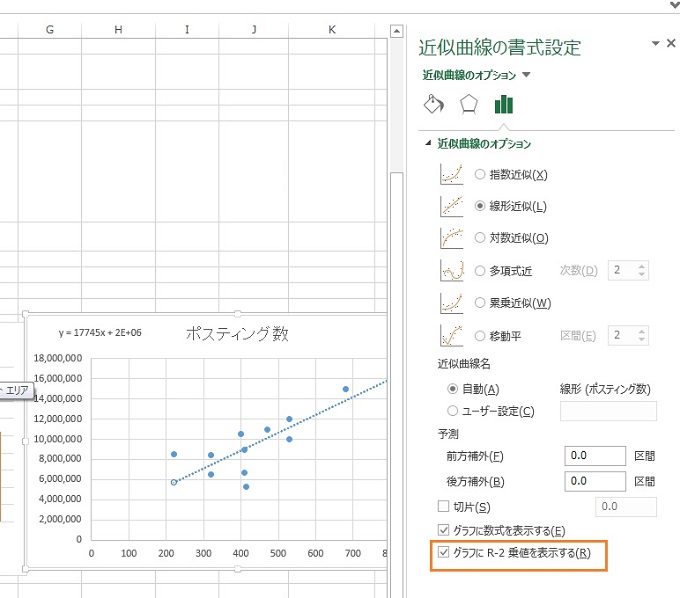
今回導きだされた関数は、実際のデータとどれだけ当てはまって説明できるかを数値化したいと思います。
R^2 = 説明出来ている情報/全情報
数式を表示する時に、『グラフにR-2乗値を表示する』にチェックを入れます。
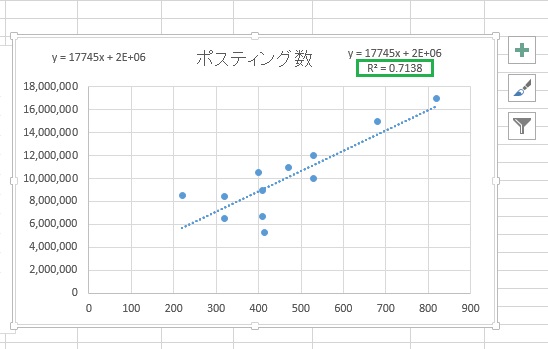
0.7138と出ましたね。
71%がこの関数で説明出来るということを表します。
決定係数の強さ
- 0.9 ~ 1 非常に当てはまる
- 0.7 ~ 0.89 強く当てはまる
- 0.5 ~ 0.69 当てはまる
- 0.5未満 あまり当てはまらない
0.7138は少し弱いが、だいたい当てはまってるなぁってところですね。
『あのさぁ!グラフもいらないし、数値だけ知りたいの!』
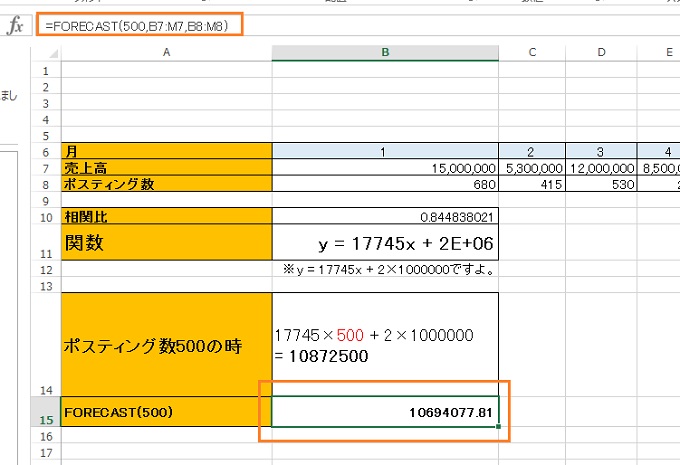
って人には、こんな風にFORECAST()関数で答えが簡単に出せます、結論から先に言うべきですよね、ごめんなさい。ただ、回り道したおかげでどうしてその数字がどうして出るのか必要に応じて説明出来るので、提案の説得力に活きてくるはずです。
色々なデータの相関関係を割り出して、未来予測をするデータとしてビジネスに役立てていければ良いですよね!
お疲れ様です。